
이런 기출 문제를 본 적이 있을 것이다. ㄷ 선지에 대해 말이 꽤 많았는데, 대부분의 해설 강의를 보면 케플러 회전 그래프 그려놓고 "밖으로 갈수록 공전속도차가 감소하니까 파장차는 1은 아닐거에요"라는 식으로 강의한다. 이건 엄밀히 말해서 옳은 풀이는 아니다. 공전속도와 시선속도는 좀 다르기 때문이다.
그러면 한 번 제대로 풀어보자. 먼저 우리가 뭘 구해야 하는지 살펴보면,
$$\left|\frac{\lambda_\mathrm{A}-\lambda_\mathrm{B}}{\lambda_\mathrm{B}-\lambda_\mathrm{C}}\right|=\left|\frac{\frac{\lambda_\mathrm{A}-\lambda_0}{\lambda_0}\times c-\frac{\lambda_\mathrm{B}-\lambda_0}{\lambda_0}\times c}{\frac{\lambda_\mathrm{B}-\lambda_0}{\lambda_0}\times c-\frac{\lambda_\mathrm{C}-\lambda_0}{\lambda_0}\times c}\right|=\left|\frac{V_\mathrm{A}-V_\mathrm{B}}{V_\mathrm{B}-V_\mathrm{C}}\right|$$
시선 속도 차의 비에다가 절댓값을 씌운것을 구하면 된다고 생각할 수 있겠다. 그러면 시선 속도를 구해보자.
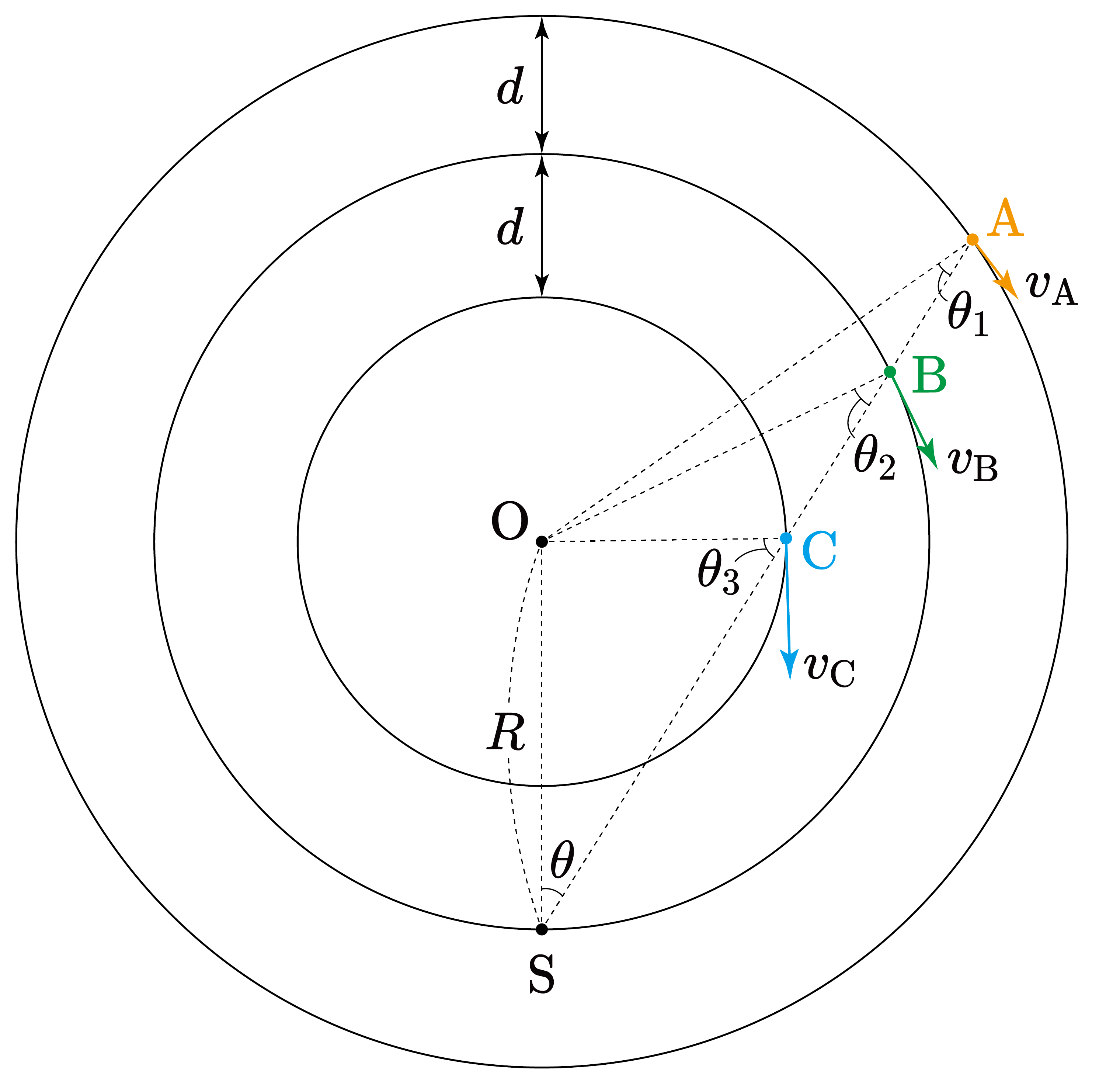
먼저 위와 같이 변수를 놓자. 문제의 조건에서 A, B, C, 태양(S)은 케플러 회전을 한다고 했으므로 $k=\sqrt{GM}$이라 하면 공전 속도는 이렇게 나타낼 수 있다.
$$v_\mathrm{A}=\frac{k}{\sqrt{R+d}},\quad v_\mathrm{B}=\frac{k}{\sqrt{R}},\quad v_\mathrm{C}=\frac{k}{\sqrt{R-d}}$$
그러면 시선 방향 성분은 이렇게 되겠다.
$$v'_\mathrm{A}=\frac{k\sin\theta_1}{\sqrt{R+d}},\quad v'_\mathrm{B}=\frac{k\sin\theta_2}{\sqrt{R}},\quad v'_\mathrm{C}=\frac{k\sin\theta_3}{\sqrt{R-d}}$$
여기서 $\triangle\mathrm{AOS}$를 주목해보자. 이 삼각형에서 사인 법칙을 적용하면
$$\frac{\sin\theta_1}{R}=\frac{\sin\theta}{R+d} \;\rightarrow\; \sin\theta_1=\frac{R\sin\theta}{R+d}$$
를 얻는다. 어차피 B는 $\theta_2=\theta$니까 넘어가고, $\triangle\mathrm{COS}$에도 똑같이 사인 법칙을 적용하고 위 식에 대입하면
$$v'_\mathrm{A}=\frac{kR\sin\theta}{(R+d)^\frac{3}{2}},\quad v'_\mathrm{B}=\frac{kR\sin\theta}{R^\frac{3}{2}},\quad v'_\mathrm{C}=\frac{kR\sin\theta}{(R-d)^\frac{3}{2}}$$
가 된다. 태양의 공전 속도는 $v_\mathrm{B}$와 같으니, 결국 시선 속도는
$$V_\mathrm{A}=\frac{kR\sin\theta}{R^\frac{3}{2}}-\frac{kR\sin\theta}{(R+d)^\frac{3}{2}},\quad V_\mathrm{B}=0,\quad V_\mathrm{C}=\frac{kR\sin\theta}{R^\frac{3}{2}}-\frac{kR\sin\theta}{(R-d)^\frac{3}{2}}$$
이다. 그러면 이걸 구하는 값에 넣어보자.
$$\left|\frac{V_\mathrm{A}-V_\mathrm{B}}{V_\mathrm{B}-V_\mathrm{C}}\right|=\frac{\frac{kR\sin\theta}{R^\frac{3}{2}}-\frac{kR\sin\theta}{(R+d)^\frac{3}{2}}}{\frac{kR\sin\theta}{(R-d)^\frac{3}{2}}-\frac{kR\sin\theta}{R^\frac{3}{2}}}=\frac{\frac{1}{R^\frac{3}{2}}-\frac{1}{(R+d)^\frac{3}{2}}}{\frac{1}{(R-d)^\frac{3}{2}}-\frac{1}{R^\frac{3}{2}}}$$
여기서 $f(x)=x^{-\frac{3}{2}}$로 놓으면 위의 값은
$$\frac{f(R)-f(R+d)}{f(R-d)-f(R)}$$
로 간단히 할 수 있다.

$y=f(x)$의 개형을 보면 분자가 분모보다 작을 수 밖에 없다는건 당연하다. 따라서 구하는 값은 1보다 작다!
'기타 > 지구과학' 카테고리의 다른 글
| 2023학년도 수능 지구과학2 주요문항 해설 (0) | 2022.11.19 |
|---|---|
| [지2] 천체가 지평선 위에 떠 있는 시간 (0) | 2022.09.17 |
| [지2] 적경 변화율 (2) | 2022.08.15 |
 planetarium
planetarium