[지2] 적경 변화율

2020학년도 9월 모의평가 지구과학I 18번

위 문제는 지구과학I에 천체가 있던 시절의 문제인데, (ㄴ) 선지의 '적경 증가율'이라는 개념이 생소하면서 흥미로워 보인다. 이 선지의 해설 강의를 들어보면 직접 지구와 행성의 위치를 그려서 선을 긋고 힘들게 푸는데, 이 글에서는 적경 증가율을 수식적으로 별도의 복잡한 개념 없이 유도해보려고 한다.

 

1. 유도

먼저 아래 그림과 같이 내행성과 외행성에서 변수를 잡아보자. 사실 이렇게 하면 황도에 대한 적경인 황경을 구하게 되는데, 알고 보면 별 문제는 없다. 실제로 적경과 황경은 크게 차이가 없기 때문. 수치적 측면에서도, 변화율 측면에서도 그렇다. 따라서 이 글에서 적경 증가율이라고 가정하고 구한 황경 증가율은 결국 적경 증가율과 사실상 같은 개념으로 취급해도 무방하다. 물론 이를 보정하는 게 아주 어려운 건 아니지만 좀 복잡하다고 봐서 생략한다.

 

내행성(왼쪽), 외행성(오른쪽)

내행성의 경우를 먼저 생각해보자. 먼저 태양의 적경은 1년에 24h만큼 증가하니까, 태양의 적경을 $\alpha_\odot=24t$로 쓸 수 있겠다. 이때 내행성의 이각을 $\theta$라 하고, 적경이 증가하는 방향으로 이동할 때, 즉 동방 이각 방향을 양(+)이라고 놓자. 또 내행성의 공전궤도반지름을 $r$, 회합주기를 $S$, 내행성이 공전한 각도를 $\theta'$이라고 놓게 되면, 일단 코사인 법칙에 의해 행성과 지구 사이의 거리를 알 수 있고, 또 사인법칙으로 $\theta$와 $\theta'$의 관계를 알 수 있다. 이렇게 하면
$$\frac{r}{\sin\theta}=\frac{\sqrt{r^2+1+2r\cos\theta'}}{\sin\theta'}$$
가 된다. 이 식을 정리하면 이각 $\theta$는
$$\theta=\arcsin\left[\frac{r\sin\theta'}{\sqrt{r^2+1+2r\cos\theta'}}\right]$$
로 쓸 수 있다. 이때 $\displaystyle\theta'=\frac{2\pi t}{S}$이고 적경은 $\displaystyle\alpha=\alpha_\odot+\frac{12}{\pi}\theta$이므로,
$$\alpha_\mathrm{inf}=24t+\frac{12}{\pi}\arcsin\left[\frac{r\sin\left(\frac{2\pi t}{S}\right)}{\sqrt{r^2+1+2r\cos\left(\frac{2\pi t}{S}\right)}}\right]$$
가 된다. 외행성도 비슷하게 생각해 볼 수 있는데, 내행성이랑 완전히 똑같이 생각하다가는 $y=\arcsin x$의 정의역이 한정되는 문제 때문에 그래프가 끊겨 나온다. 그래서 사인법칙을 다른 각에 대해 써서 유도하면

$$\alpha_\mathrm{sup}=24t\left(1-\frac{1}{S}\right)+\frac{12}{\pi}\arcsin\left[\frac{\sin\left(\frac{2\pi t}{S}\right)}{\sqrt{r^2+1+2r\cos\left(\frac{2\pi t}{S}\right)}}\right]$$

로 구할 수 있다. 참고로 inf는 inferior의 약자이고, sup는 supreme의 약자이다.

---

2. 적용

위에서 구한 식으로 그린 금성과 화성의 적경 및 적경 증가율 그래프이다.

 

금성의 적경과 적경 증가율

화성의 적경과 적경 증가율

내행성의 적경변화는 외합에서 최대이고, 외행성의 적경변화는 합에서 최대임을 알 수 있다. 역행보다 순행이 더 빠르게 나타나기도 하다. 그리고 내행성과 달리, 외행성은 태양(24h/yr)보다 빠른 적경 변화를 보이지 않는다는 것도 알 수 있다. 당연하다면 당연한게, 외행성은 항상 뜨는/남중하는/지는 시간이 빨라지니까, 태양에 대해 적경이 감소하는 방향(동→서)로 이동하니까. 한편 내행성의 역행은 최대이각과 꽤나 떨어진 위치에서 일어나는 걸 확인할 수 있다. 즉, '최대이각 부근에서 역행한다'는 말은 옳지 않고, '내합 부근에서 역행한다'가 맞는 표현이겠다.

 

이제 모든 태양계 행성의 적경 증가율 그래프를 보면,

 

내행성의 적경 증가율

외행성의 적경 증가율

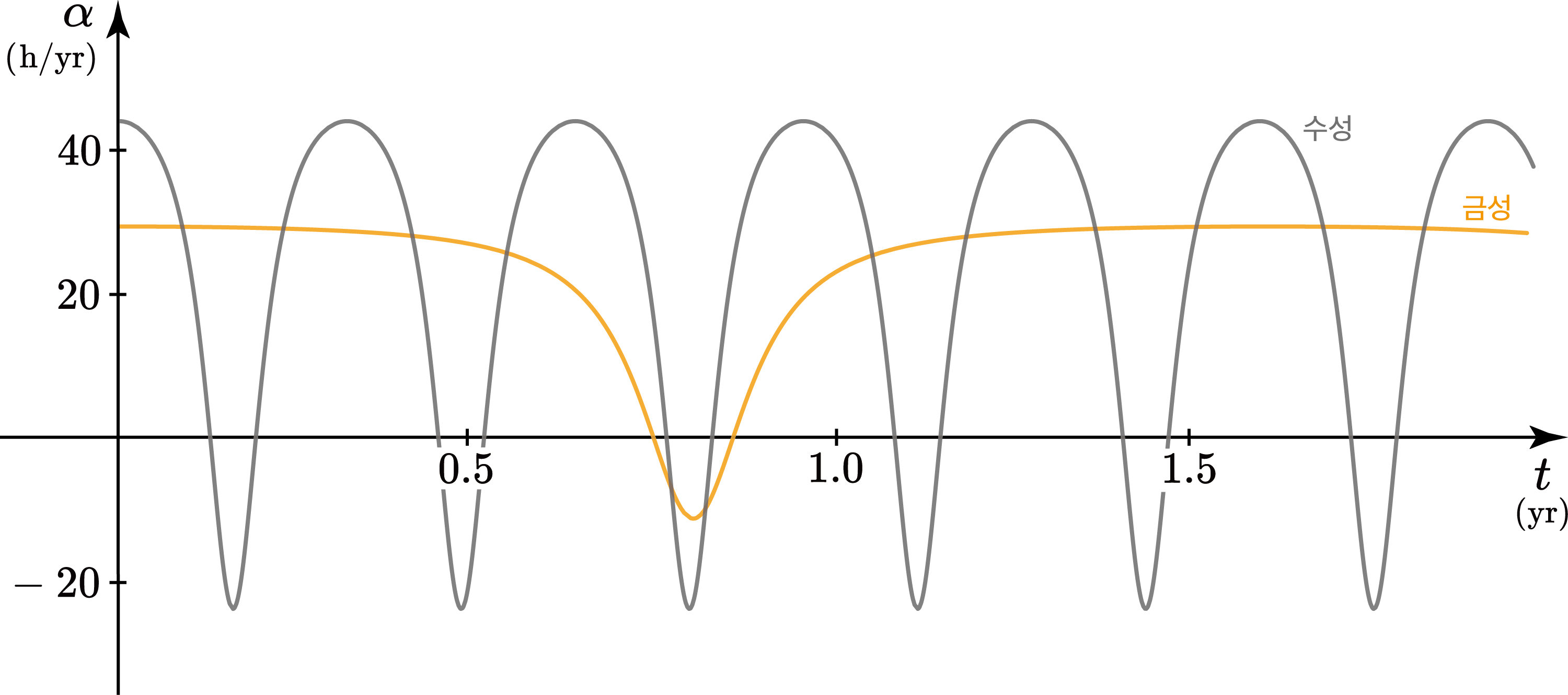
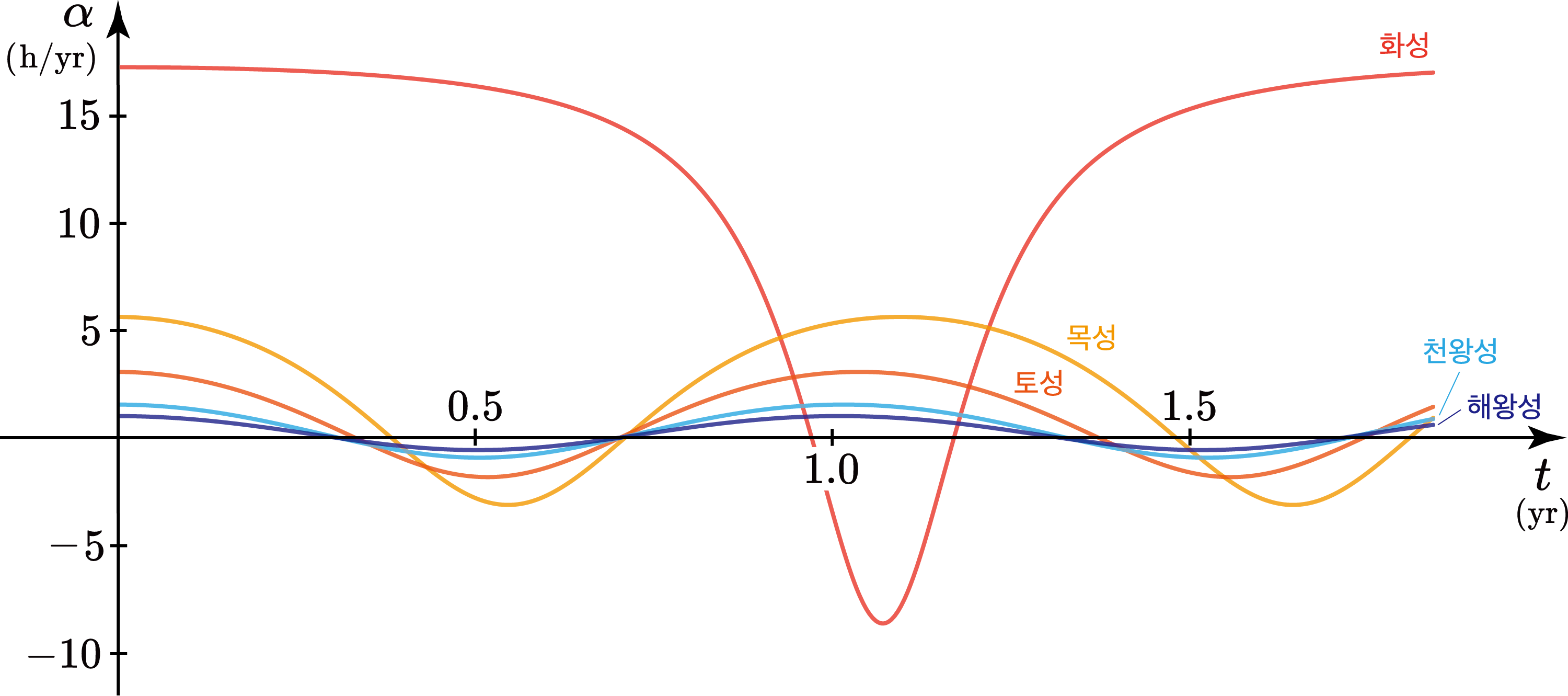
이렇게 나타난다. 내행성은 지구에서 멀수록 적경 변화 그래프의 진폭이 크다. 지구에서 멀수록 천구상에서 더 빨리 움직인다는 이야기이다. 수성은 그 회합주기가 짧은 만큼 태양에 대해 빠른 이각 변화를 보이니까 그렇다. 한편 외행성은 지구에서 멀수록 적경 변화 그래프의 진폭이 작다. 지구에서 멀수록 천구상에서 더 느리게 움직인다는 이야기이다. 배경별은 어떻게 보면 지구로부터의 거리가 무한대(∞)인 행성과도 같다는 걸 생각해 보면 당연한 이야기다.

 

이렇게 적경 증가율에 대한 이야기를 해보았다. 식을 알 필요는 없지만, 그래프의 특징 정도는 기억해 두면 쓸만하지 않을까? 예를 들어 합에서 얼마나 움직였나를 보고 어떤 행성인지 판단하거나...?