2023학년도 수능 지구과학2 주요문항 해설

3번 (29%)

기존의 3번에 비하면 쉬운 문제는 아닙니다. 저기압에 의한 해수면 상승을 다루었는데, 정역학 평형 공식만 적용하면 하나도 어렵지 않긴 합니다만 문제 번호가 번호인만큼 살짝 당황했을 수 있습니다. 물어보는 형식 역시 기존 평가원 스타일과는 차이가 있습니다.

 

해설

먼저 저기압이 통과하면 해수면에 작용하는 기압이 감소하고, 고기압이 통과하면 증가합니다. 따라서 전자의 경우 해수면 높이가 상승하고 후자의 경우 하강하게 됩니다. 한편, 10hPa이 변화하였다고 하므로 변화의 방향성을 무시할 때 해수면 높이 변화량의 크기는

$$\Delta h=\frac{\Delta P}{\rho \mathrm{g}}=\frac{10\times10^2\;\mathrm{Pa}}{1000\;\mathrm{kg/m^3}\cdot10\;\mathrm{m/s^2}}=0.1\;\mathrm{m}$$

입니다. 따라서 2번이 답입니다.

---

7번 (41%)

전형적인 지상풍 문제이지만, 제시 방식이 특이합니다. 평가원은 지금까지 지구자전각속도와 위도를 따로 제시하지 않고 코리올리인자($f=2\Omega \sin\phi$)만을 제시한 적이 없습니다. 그렇기에 흥미로운데, 이건 4페이지의 19번에서도 그대로 이어집니다.

 

해설

북풍 계열의 지상풍이 불고 있다면, 경우는 두가지 입니다. 먼저 북동풍이 부는 경우 등압선에 대해 풍속 벡터와 전향력 벡터가 같은 방향을 향하게 됩니다. 이러면 마찰력과 전향력의 합력이 기압경도력의 반대 방향으로 작용할 수가 없습니다. 따라서 A에서는 북서풍이 불어야만 합니다.

 

ㄱ. 북서풍이 불기 때문에 기압 경도력은 동쪽으로 작용하며, 따라서 기압은 서쪽이 더 높습니다. (참)

 

ㄴ. 간단한 벡터 분해를 통해 전향력은 기압경도력의 절반, 마찰력은 기압경도력의 $\frac{\sqrt{3}}{2}$배임을 알 수 있습니다. (거짓)

 

ㄷ. 위에서 전향력이 기압경도력의 절반이므로, $P_\mathrm{H}=2C$에서

$$\frac{1}{1.0\;\mathrm{kg/m^3}}\cdot\frac{4\times10^2\;\mathrm{Pa}}{d\;\mathrm{m}}=2\cdot10^{-4}\;\mathrm{/s}\cdot10\;\mathrm{m/s}$$

이므로, $d$는 200km임을 얻습니다. (거짓)

---

10번 (31%)

지질도 문제인데, 작년 수능에서 잠깐 보여주었던 "그 경사"가 핵심 포인트로 등장했습니다. 항상 지층 경계면의 경사 방향이 지표의 경사 방향과 동일한 경우 주의하여야 합니다. 둘의 경사 방향이 같을 때, 지질도 상에서 지층 경계선이 등고선을 뚫고 들어가는 형태가 보일 경우 주향선 간격이 등고선 간격보다 넓게 되어 지층 경계면의 경사가 지표 경사보다 완만하게 그려지기 때문입니다.

 

해설

ㄱ. 지질 기호에 의해 A의 경사 방향은 남서쪽입니다. (참)

 

ㄴ. 지표 경사와 지층 경계면 경사가 남서쪽으로 같은 상황에서 지층 경계면 경사가 더 완만합니다. 따라서 이를 고려하여 지질단면도를 간단하게나마 그려보면, 생성 순서는 C, B, A 순임을 알 수 있습니다. (참)

 

ㄷ. 단층의 경사 방향이 남서쪽이므로 단층선 남쪽의 지층이 북쪽의 지층을 덮고 있는 형태가 됩니다. 따라서 단층선 남쪽의 지층이 상반, 북쪽의 지층이 하반에 해당합니다. 이때 B와 C의 지층 경계면이 단층선과 만나는 점을 살펴볼 때, 상반이 하반에 대해 상대적으로 올라간 것이 보입니다. 따라서 역단층이 나타납니다. (거짓)

---

14번 (37%)

문제가 결코 어려운 것은 아니지만 자료의 모양이 평가원 방식과 살짝 차이가 있습니다. 오히려 임용고시에 가까운 형태라고 불러야 할 것입니다. 세 범례와 그 오차까지 모두 나타낸 실측 자료인데, 꽤 험악하게 생겨 당황할 수 있습니다.

 

해설

ㄱ. 해당 구간에서의 전체적인 회전 속도 분포를 보아, 거리가 증가함에 따라 속도가 작게나마 증가하고 있으므로 케플러 회전은 절대 아닙니다. (거짓)

 

ㄴ.  어떤 천제의 공전 속도, 공전 궤도 반지름에 대해 공전 궤도 안쪽의 누적 질량은

$$M=\frac{rv^2}{G}$$

로 표현됩니다. 물론 궤도 바깥쪽의 질량이 회전 속도에 영향을 주어 이 식이 정확하게 성립하는 것은 아니지만, 대략적으로 맞습니다. 어쨌거나 a와 b의 거리비는 1:3이고 공전 속도는 a가 더 큽니다. 따라서 위 식에 의해 $M_\mathrm{b}$는 $M_\mathrm{a}$의 3배보다 작습니다. (거짓)

 

ㄷ. 회전 속도로 추정한 질량은 암흑물질까지 고려한 실제 질량이고, 빛을 내는 천체들의 총질량은 암흑물질을 고려하지 않은 질량이므로 당연히 맞는 선지입니다. (참)

---

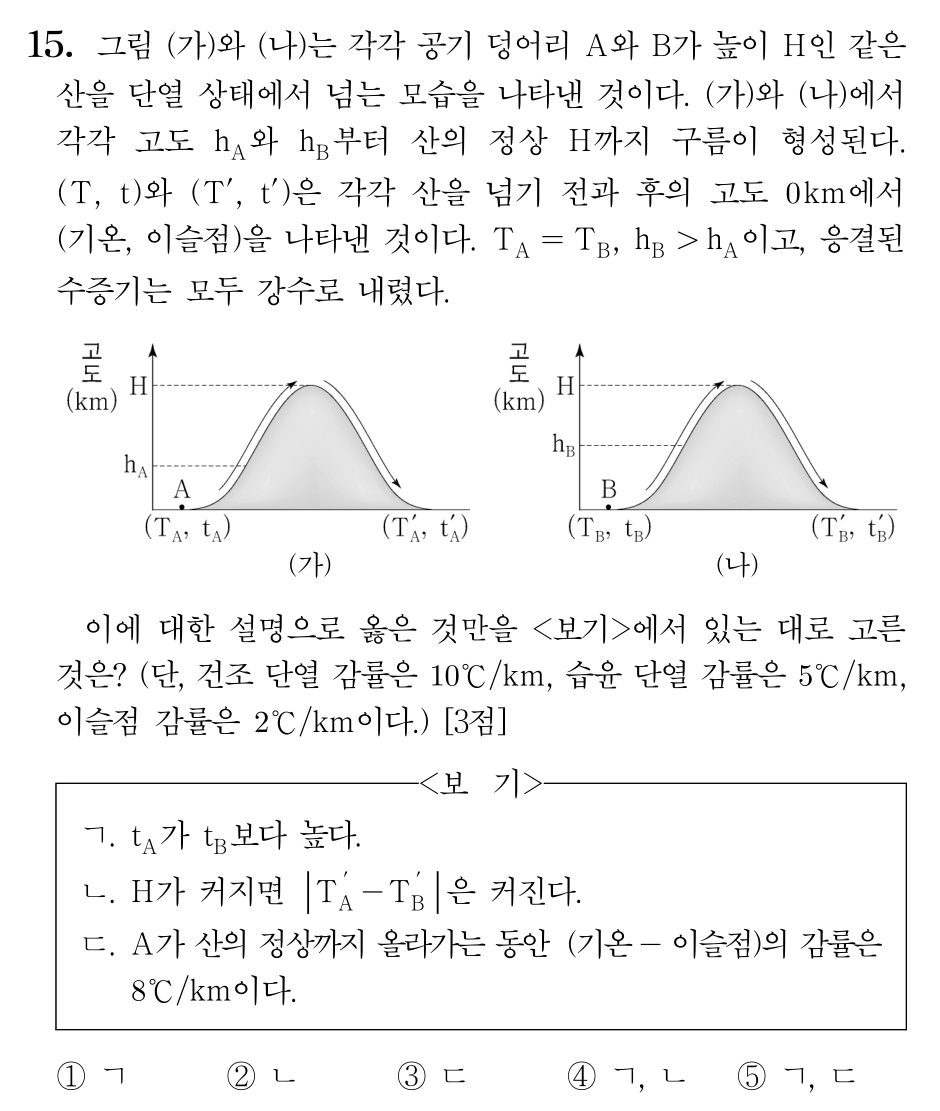
15번 (41%)

그냥 숫자로 나왔으면 수월하게 풀었을 문제입니다. 그러나 숫자가 하나도 없고 모든 것을 변수로 주어 그냥 풀기에는 막막했을 수 있습니다. 실제로 오답률이 낮지 않습니다. 이런 문제는 크게 두가지 풀이가 있을 수 있는데, 첫번째는 아무 숫자나 넣어서 푸는 것이고 두번째는 변수를 그대로 적용해 푸는 것입니다. 첫번째 풀이가 시간이 짧게 걸려서 좋을 수 있지만 항상 맞는 답이 나온다는 보장이 없습니다. 따라서 두번째 풀이로 빠르게 푸는 연습을 해야 합니다.

 

해설

ㄱ. 온도가 $T_\mathrm{A}=T_\mathrm{B}$인 상황에서 상승응결고도는 $h_\mathrm{A}<h_\mathrm{B}$입니다. 상승 응결 고도는 $T-t$에 비례하므로, $t_\mathrm{A}>t_\mathrm{B}$입니다. (참)

 

ㄴ. 먼저 수식 풀이를 보여드리겠습니다. $T_\mathrm{A}=T_\mathrm{B}$우리는

$$T_\mathrm{A}-10h_\mathrm{A}-5(H-h_\mathrm{A})+10H_\mathrm{A}=T'_\mathrm{A}$$

임을 알기 때문에, 이를 정리하면 $T_\mathrm{A}'=T_\mathrm{A}+5(H-h_\mathrm{A})$를 얻습니다. 따라서

$$|T_\mathrm{A}'-T_\mathrm{B}'|=|5(h_\mathrm{A}-h_\mathrm{B})|$$

가 되므로, 이 값은 $H$와는 관계 없다는 사실을 알 수 있습니다. 이제 그림 풀이를 보면, 간단히 단열선도를 그리면

대충 이런 느낌입니다. 보시면 $|T_\mathrm{A}'-T_\mathrm{B}'|$는 $H$와 관계 없이 이슬점이 원래 낮았던 쪽의 상승응결고도부터 고정된 값이 되는 것을 확인할 수 있습니다. (거짓)

 

ㄷ. 수증기의 응결이 시작되면 기온은 이슬점과 같은 감률(=습윤단열감률)로 변하므로, 당연히 틀린 선지입니다. (거짓)

---

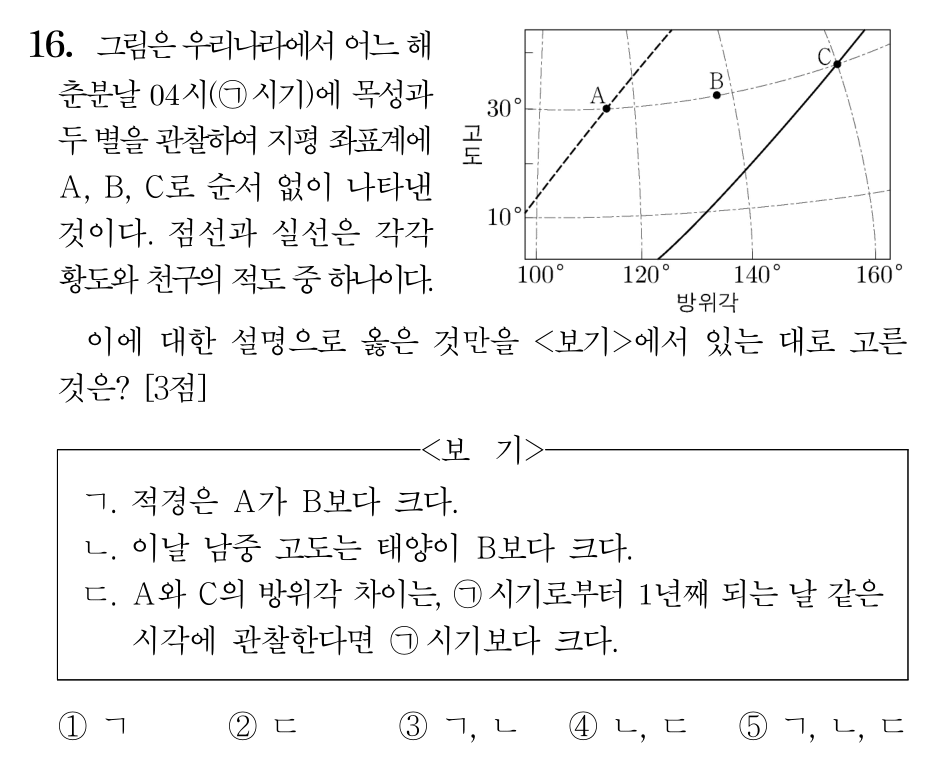
16번 (53%)

엄청나게 문제는 아닌데, 그렇다고 절대 쉬운 문제도 아닙니다. 문제를 관통하는 핵심 논리는 기존의 행성 문제와 별 다를바가 없으나, 왠지 모르게 푸는 것이 쉽지는 않습니다. 역시나 높은 오답률이 이를 증명합니다. 아무래도 기존의 논리를 재활용했지만 그 논리를 한 문제에 엮어 놓은 것이 난이도를 높였던 것 같네요. 특히 ㄷ이 흥미롭습니다.

 

해설

가장 먼저 무엇이 황도인지 판별해 봅시다. 천구의 적도가 지평선과 만나는 점인 동점과 서점은 그 방위각이 항상 90도와 270도로 일정합니다. 그렇기에 지표와 만나는(또는 그 부근)의 방위각이 120도에 가까운 실선은 천구의 적도가 아닌 황도입니다. 따라서 황도에 위치한 C는 목성이고, A와 B는 별입니다. (행성은 황도에서 6도를 벗어나지 않습니다.)

 

ㄱ. 춘분날 04시에 관찰한 동쪽 하늘의 모습이기에 이 부근의 적경은 12h와 24h 사이일 것입니다. 따라서 적경은 A가 B보다 큽니다. (참)

 

ㄴ. 적위는 태양이 0, B가 음(-)입니다. 따라서 남중 고도는 태양이 B보다 큽니다. (참) 

 

ㄷ. C는 목성, 즉 외행성이므로 뜨고/남중하고/지는 시각이 매일 빨라집니다. 따라서 같은 시각에 관측하면, C는 시계방향으로 움직이는 것처럼 보일겁니다. 이때 회합주기만큼이 지나면 다시 원래 위치로 돌아올 것입니다. (회합주기란 태양과의 상대적 위치관계의 주기이며, 시간이란 태양에 의해 정의되기 때문에 같은 시각에 같은 위치로 돌아오는 주기는 회합주기입니다.) 그런데 목성의 회합주기는 1년보다 깁니다. 따라서 1년 동안 목성은 같은 시각에 관측했을 때 한바퀴를 채 돌지 못합니다. 그러므로 지금으로부터 1년째 되는 날, C는 현재 위치에 비해 더 동쪽에 가깝게 위치하여야 합니다. 한편 A는 별이므로 1년에 한바퀴를 연주하여 방위각 변화는 없습니다. 이를 종합하면 A와 C의 방위각 차이는 감소합니다. (거짓)

 

---

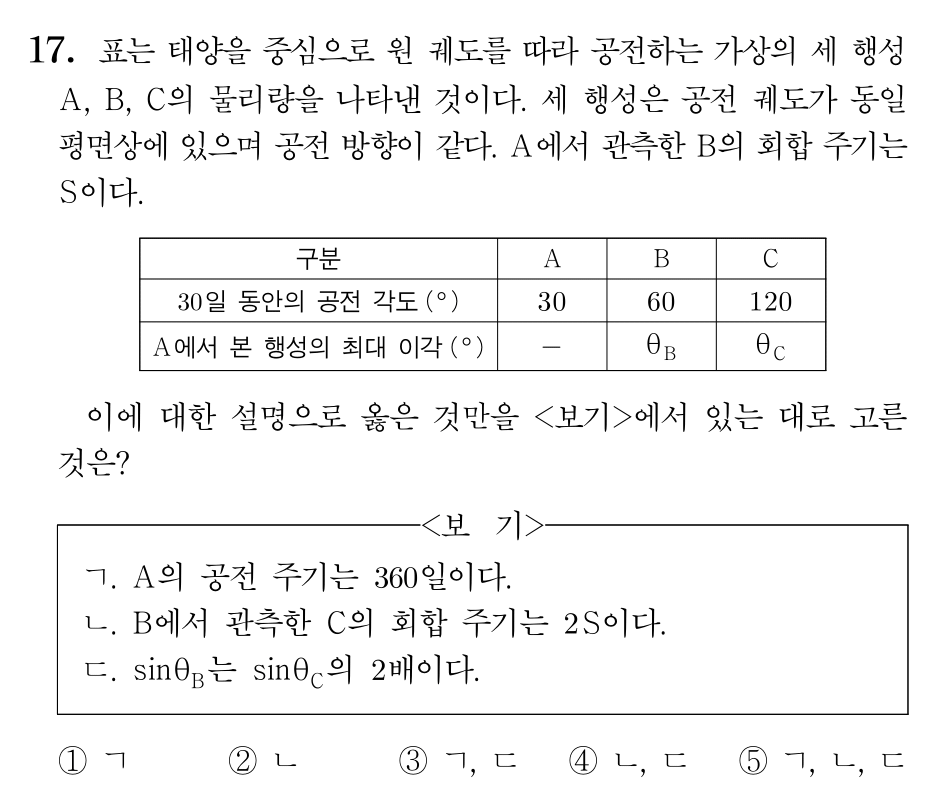
17번 (36%)

어렵지 않은 문제이지만, 기존의 회합주기 문제와는 스타일의 차이가 있습니다. 보통 회합주기 문제는 단독으로 나오면 일종의 퍼즐 형태로 출제되었고, 또는 행성 문제와 연관되어 출제되었습니다. 그러나 202309에서 볼 수 있듯이 평가원은 공전 각도와 관련한 소재를 행성의 공전궤도 반지름과 연관지어 새롭게 출제하고 있습니다. 이는 2015 개정 이후로 지구과학II에 새롭게 추가된 내용이기에 이를 적극적으로 출제하는 것으로 보입니다.

 

해설

ㄱ. A는 30일 동안 30도를 공전하므로, 360도를 공전하는 데에는 360일이 걸립니다. (참)

 

ㄴ. 위와 같은 방법으로 B와 C의 공전 주기는 각각 180일, 90일입니다. 따라서 간단한 계산을 통해 A에서 관측한 B의 회합주기는 360일이며 B에서 관측한 C의 회합주기는 180일임을 알 수 있습니다. 따라서 360일이 S라면, B에서 관측한 C의 회합주기는 0.5S입니다. (거짓)

 

ㄷ. A의 공전 궤도 반지름이 $R$, 어떤 행성의 공전 궤도 반지름이 $r$, A에서 관측한 그 행성의 최대이각이 $\theta$라면 $r=R\sin\theta$임을 간단한 그림을 통해 보일 수 있습니다. 따라서 $\sin\theta$는 오직 $r$에만 비례합니다. 그런데 공전 주기는 B가 C의 2배이므로, 케플러 제3법칙에 의해 공전 궤도 반지름은 B가 C의 2배가 아닙니다. 그러므로 $\sin\theta$ 역시 B가 C의 두배가 아닙니다. (거짓) 

 

---

19번 (55%)

이 시험지에서 가장 어려운 문항입니다. 기압 경도력에 대한 정확한 이해와 어느정도의 계산이 요구되는 문제로, 절대 만만한 문제가 아니지만 의외로 어렵다고 느낀 학생이 적습니다. 사실 그 이유를 잘 모르겠으나 정확하지 않은 방법으로 풀었지만 답은 나왔을 가능성이 있고, 또는 실제로 어렵다고 느끼지 않았을 수 있습니다.

 

해설

ㄱ. A가 가열되었고 C가 냉각되었으므로, 지상 기압이 1000hPa로 일정한 상태에서 600hPa 등압면은 동쪽으로 기울어지게 됩니다. 따라서 600hPa 등압면상에서 기압 경도력은 북쪽으로 작용하므로 지균풍의 풍향은 서풍 계열입니다. (거짓)

 

ㄴ. 1000hPa의 단위 면적의 지표로부터 600hPa 등압면까지 연직으로 세워진 공기 기둥의 질량은 지표와 등압면의 기압차 $\Delta P=400\;\mathrm{hPa}$, 높이차 $\Delta h$에 대해

$$\frac{m}{A}=\frac{\rho A\Delta h}{A}=\rho\Delta h=\frac{\Delta P}{\mathrm{g}}=4000\;\mathrm{kg/m^2}$$

입니다. (참)

 

ㄷ. 먼저 선지가 무엇을 의미하는지 확인해봅시다. A와 C의 지표에서 600hPa 등압면의 고도차를 $\Delta H$, 600hPa 등압면의 기울기를 $\tan\theta$, 코리올리인자를 $f=2\Omega\sin\phi$라 하면$$v=\frac{\mathrm{g}}{f}\tan\theta=\frac{10\;\mathrm{m/s^2}}{10^{-4}\mathrm{/s}}\cdot\frac{\Delta H}{2000\times10^3\mathrm{m}}=\frac{\Delta H}{20}$$이므로, 이 값이 20m/s보다 크다는 것은 $\Delta H$가 400m보다 크냐고 묻는 것과 동치입니다. 이때 정역학 방정식에 의해 A와 C에서 지표에서 등압면까지의 높이는 각각 $\Delta h_\mathrm{A}=\frac{\Delta P}{\rho_\mathrm{A} \mathrm{g}}$와 $\Delta h_\mathrm{B}=\frac{\Delta P}{\rho_\mathrm{B} \mathrm{g}}$이므로, 

$$\begin{align}\Delta H&=\Delta h_\mathrm{A}-\Delta h_\mathrm{B}\\&=\frac{\Delta P}{\mathrm{g}}\left(\frac{1}{\rho_\mathrm{A}}-\frac{1}{\rho_\mathrm{B}}\right)=400\cdot\frac{10}{11}\end{align}$$

임을 계산할 수 있습니다. 이 값은 400m보다 작으므로, 풍속은 20m/s보다 크지 않습니다. (거짓)

---

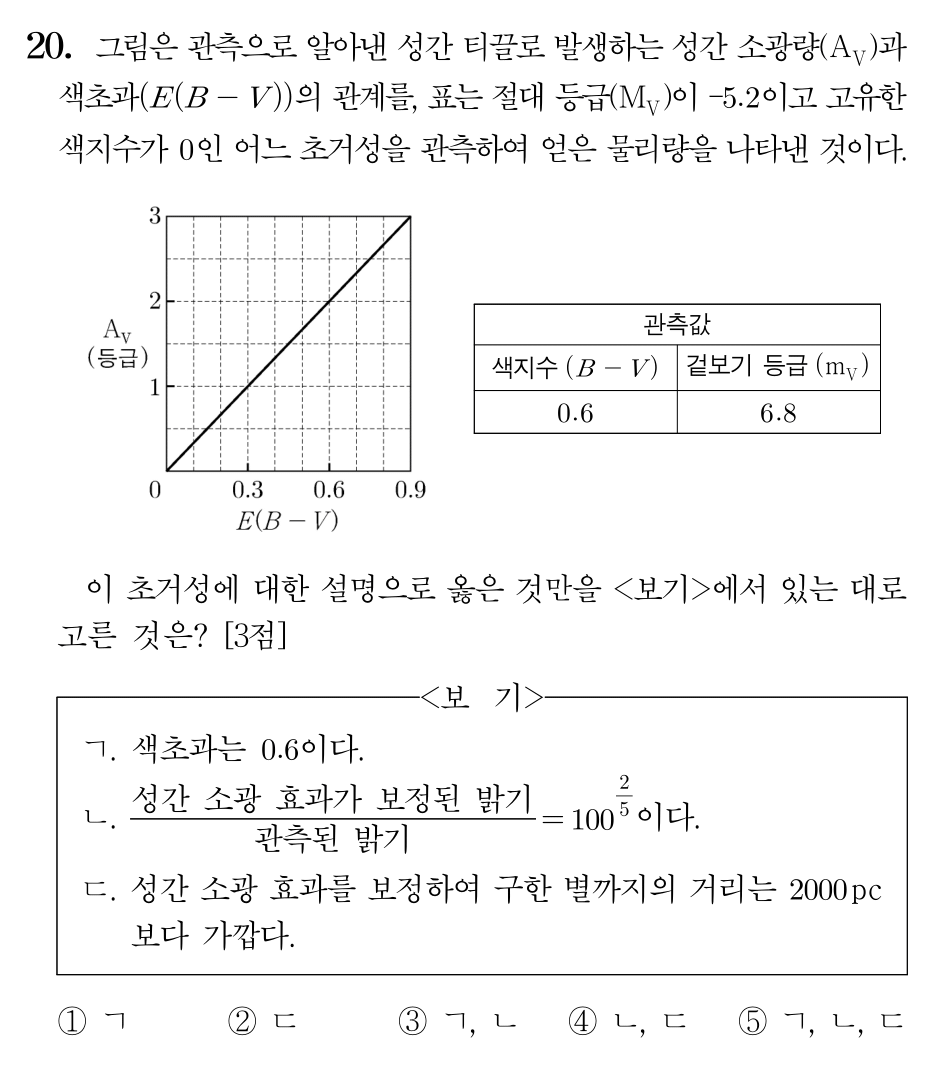
20번 (47%)

문제는 쉬운데 자료의 제시 방식이 대단히 임용고시스럽습니다. 색초과와 성간소광의 비례상수를 제시하는 것은 전통적인 임용고시 방식이고, 수능에는 출제된 적이 없습니다.

 

해설

ㄱ. 관측 색지수는 0.6, 고유 색지수는 0이므로 색초과는 0.6입니다. (참)

 

ㄴ. $\mathrm{E}(B-V)=0.6$이므로 $A_\mathrm{v}=2$입니다. 따라서 포그슨 방정식에 의해

$$A_\mathrm{v}=m_\mathrm{v}-m_\text{보정값}=2.5\log\left(\frac{m_{\text{보정값}}}{m_\mathrm{v}}\right)$$

이고, 이를 계산하면 $\frac{m_{\text{보정값}}}{m_\mathrm{v}}=100^\frac{2}{5}$입니다. (참)

 

ㄷ. 성간 소광량이 2등급이므로, 성간 소과 효과를 보정한 겉보기 등급은 4.8등급입니다. 따라서

$$m_\text{보정값}-M_\mathrm{v}=10=5\log r-5$$

이므로, $r$은 1000pc입니다. (참)