24학년도에 비해 확실히 어렵게 나왔고, 신유형이 꽤 있어서 현장에서 당황했을 법합니다. 다만 이는 어디까지나 현재의 기준이고, 과거 지2를 기준으로 본다면 살짝 어렵게 나온 정도라고 할 수 있겠습니다. 해설은 제가 보기에 어렵거나 흥미로운 신유형 문제들을 넣었습니다.

13번 (48%)
ㄷ이 흥미로운 문제로, 선지 배치도 그렇고 ㄷ의 참/거짓 판단이 핵심인 문제입니다. 감으로 풀 수도 있지만 정확하게 푸는게 더 중요하다고 생각하므로 정확한 풀이를 첨부합니다.
해설
ㄱ. 남반구에서 수평 수압 경도력이 동쪽으로 작용한다면 지형류는 북쪽으로 흐릅니다. (참)
ㄴ. 단위 질량당 연직 수압 경도력의 크기는 중력가속도($\mathrm{g}$)와 같으므로, P와 Q에서 같습니다. (거짓)
ㄷ. 먼저 A와 B에서 압력 식을 써봅시다.
$$\rho_1\times (3+300)=\rho_2\times(300)$$
또 같은 식을 평균 밀도로 써봅시다. 평균 밀도이므로 물 기둥 전체를 써줘야 합니다.
$$\rho_\mathrm{A}\times(3+400+300+300)=\rho_\mathrm{B}\times(400+300+300)$$
두 식을 간단히 하면,
$$\rho_1=\frac{300}{303}\rho_2$$
$$\rho_\mathrm{A}=\frac{1000}{1003}\rho_\mathrm{B}$$
이고, 두 식을 연립하면
$$|\rho_\mathrm{A}-\rho_1|=\left|\frac{1000}{1003} \rho_\mathrm{B}-\frac{300}{303} \rho_2\right|<|\rho_\mathrm{B}-\rho_2|$$
이므로, $|\rho_\mathrm{A}-\rho_1|<|\rho_\mathrm{B}-\rho_2|$입니다. (거짓)

15번 (49%)
역시 ㄷ이 흥미롭습니다. 그림만 잘 봤다면 어렵진 않겠지만, 물어보는 방식이 생소해서 헷갈리기 쉽습니다.
해설
심해파는 해저로 갈수록 물 입자의 운동 반지름이 작아지며, 이심률이 변하지 않고 계속 원운동을 합니다. 한편 천해파는 해저로 갈수록 물 입자의 운동 장반경은 일정하게 유지되는 반면 단반경은 작아집니다. 즉, 이심률이 커집니다. 따라서 ㉠은 심해파, ㉡은 천해파입니다.
ㄱ. ㉠은 심해파입니다. (참)
ㄴ. ㉡, 즉 천해파의 물 입자 운동은 해저면의 영향을 받습니다. (참)
ㄷ. 파고는 물 입자의 운동 궤적의 단반경의 두 배이므로, 결국 단반경과 관련이 있습니다. 즉, ㄷ에서 말하는 식은 (장반경/단반경)을 간접적으로 의미한다고 볼 수 있습니다. 이때 좌변은 1(원 운동)이고 우변은 1보다 크므로(타원 운동) (좌변) < (우변)입니다. (참)

16번 (39%)
문제 자체의 형식이 상당히 새롭습니다. 그림도 없고, 단순히 3개의 정보만 주는 문제라 색다릅니다. 그래도 줄 정보는 다 주었고 아는 범위 내에서 어렵지 않게 해결할 수 있으니, 말려들지 않는다면 괜찮습니다. 물론 생소함 때문에 말려들기는 쉬울 수 있고, 실제로 정답률이 매우 낮습니다.
해설
고유 색지수는 $0.5$이고 색초과는 $1.0$이므로
$$(B_0+\Delta B)-(V_0+\Delta V)=1.5$$
입니다. 이때 별까지의 실제 거리가 $r=1000\;\mathrm{pc}$이고 $M_V=4.5$이므로
$$V_0-M_V=5\log r-5$$
에서
$$V_0=14.5$$가 됩니다. 그런데 V등급의 변화는 색초과의 3배, 즉 3.0이므로
$$V_0+\Delta V=17.5$$
입니다. 이를 첫 번째 식에 대입하면
$$B=B_0+\Delta B=17.5+1.5=19.0$$
입니다.

17번 (42%)
의외로 쉽지 않은 문제이긴 하지만, ㄱ이 실제 푸는 논리에 비해 누가 봐도 강체 회전은 아니라 그렇게 어렵다고 느끼지 않았을 가능성이 높습니다. 그래서 자세히 파고들면 얻어갈 것이 많습니다.
해설
ㄱ. 일단 가장 직관적으로 풀자면, 은하가 강체회전하기 위해서는 누적 질량이 가파르게 쌓여야 하며, 누적질량이 거의 변하지 않는다면 거리에 따라 질량이 쌓이지 않는다는 것으로 결국 케플러회전에 가까운 양상을 가집니다. 따라서 이 구간에서는 강체회전은 아니겠네요. 그렇다면 정확히 풀어봅시다.
문제의 조건은 "별에 작용하는 만유인력은 해당 궤도 안쪽의 질량이 작용하는 만유인력과 같다"라는 사실을 의미하는데, 이로 인해
$$v=\sqrt{\frac{GM}{r}}$$
이 성립하며, 이때 $M$은 $r$ 안의 모든 질량의 합, 즉 누적 질량입니다. 이는 $r$ 안쪽의 질량에 의한 만유인력과 $v$의 속도로 $r$의 궤도를 도는 데에 의한 구심력이 같다는 식에서 쉽게 도출할 수 있으며, 단순 케플러 회전뿐만 아니라 원운동 전반에 쓰일 수 있는 식입니다. 만일 물체가 강체 회전을 한다면 $v=r\omega$이고 $\omega$는 일정한 상황일 텐데, 이를 위 식에 대입하면
$$M=\frac{r^3\omega^2}{G}$$
의 꼴이므로 누적 질량은 일정한 회전 각속도에 대해 회전 반지름의 세제곱에 비례하는 꼴이어야 합니다. 그러나 A는 전혀 그렇게 보이지 않으므로 강체 회전이라고 볼 수 없습니다. (거짓)
ㄴ. a와 b 사이의 특정 구간에 존재하는 물질의 총질량은 (b에서의 누적 질량) - (a에서의 누적 질량) 으로 구할 수 있습니다. 즉 해당 그래프의 기울기와 밀접한 연관이 있으므로, 해당 구간에서의 총 질량은 A가 B보다 작습니다. (참)
ㄷ. 위에서 살펴본
$$v=\sqrt{\frac{GM}{r}}$$
를 통해, 같은 거리($4\;\mathrm{kpc}$)에서 총질량비를 고려하면 회전 속도는 A가 B의 $\sqrt{2}$배 임을 알 수 있습니다.
이때 주기는 (공전 궤도 둘레) / (공전 속도) 이므로, 같은 둘레에 대해 회전 속도가 A가 B의 $\sqrt{2}$배이므로 공전 주기는 B가 A의 $\sqrt{2}$배입니다. (거짓)
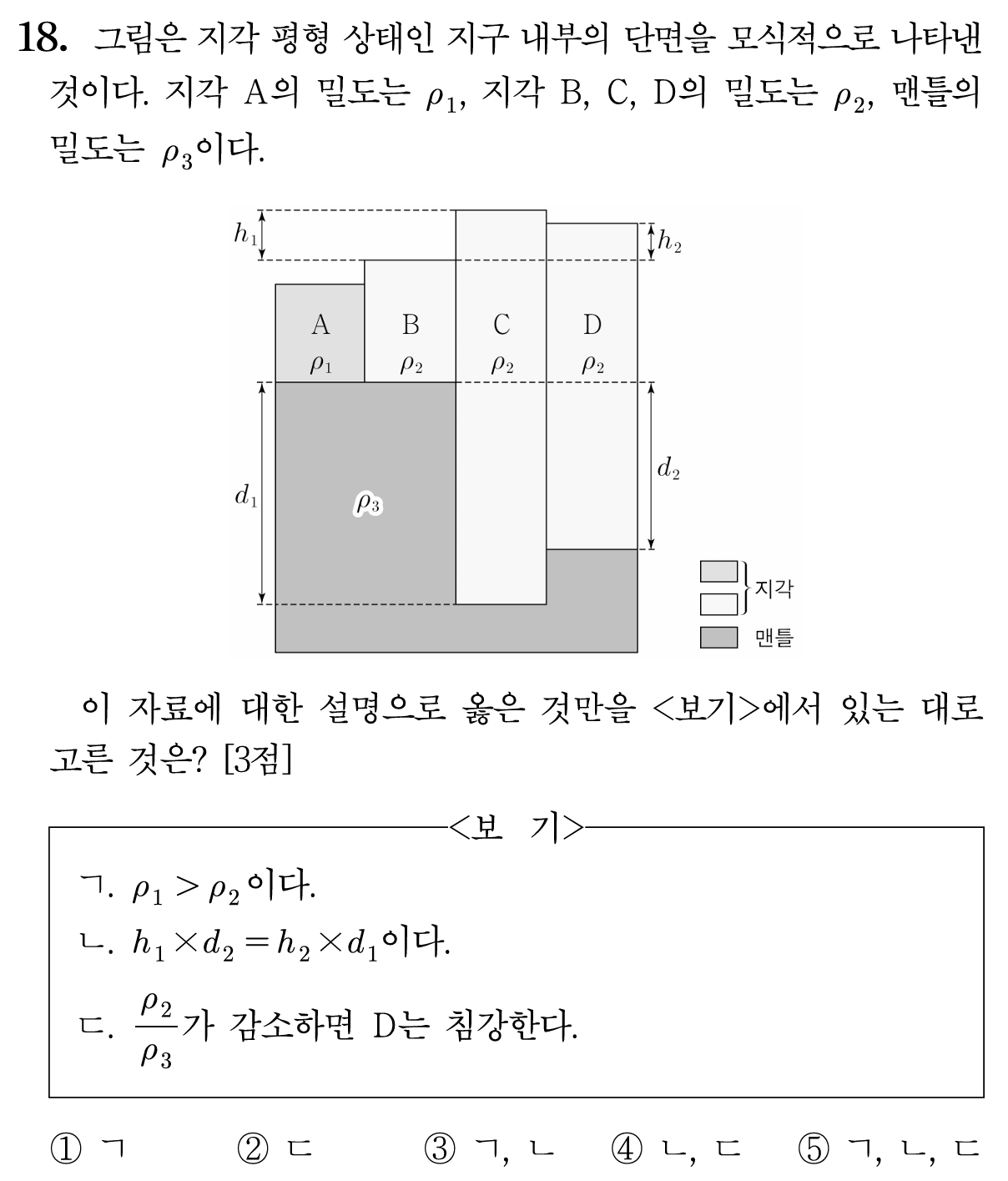
18번 (47%)
ㄴ이 싸가지가 없는 문제인데, 의외로 ㄷ도 좀 어려워 전체적인 난이도가 높습니다. 개인적으로 이번 수능의 킬러 문제가 아니었나 싶네요.
해설
ㄱ. A와 B에서 하단부의 맨틀의 두께는 같으나
지각의 두께는 $\rho_1$이 $\rho_2$의 지각보다 얇으므로, $\rho \mathrm{g} h$에서 $\rho_1>\rho_2$입니다. (참)
ㄴ. 우선 B와 C를 비교하면,
$$\rho_3 d_1=\rho_2(h_1+d_1)$$
에서
$$(\rho_3-\rho_2)d_1=\rho_2 h_1$$
입니다. 한편 B와 D를 비교하면,
$$\rho_3 d_1=\rho_2(h_1+d_2)+\rho_3(d_1-d_2)$$
이므로
$$(\rho_3-\rho_2)d_2=\rho_2 h_2$$
입니다. 따라서 첫 번째로 얻은 식과 두 번째로 얻은 식을 연립하면
$$\frac{h_1}{d_1}=\frac{h_2}{d_2}=\frac{\rho_3-\rho_2}{\rho_2}$$
입니다. (참)
ㄷ. 지각이 융기 또는 침강하는 상황이므로 $\rho_3$를 고정시키고 $\rho_2$를 움직여봅시다. 이때 $\frac{\rho_2}{\rho_3}$가 감소한다는 것은 $\rho_2$가 감소한다는 것입니다.
절대적인 기준, 즉 변하지 않는 값인 A와 비교할 때, D에서 $\rho_2$가 감소하면 그만큼 이를 $\rho_3$가 보완해주어야 하므로 D에서 $\rho_3$가 차지하는 범위인 $(d_1-d_2)$가 늘어나야 합니다. 그래야 $\rho_2$의 감소폭만큼 $\rho_3$가 등압력면에서의 압력이 변하지 않도록 채워줄 수 있기 때문입니다.
따라서 $(d_1-d_2)$가 늘어난다는 것은 지각이 융기한다는 것을 의미합니다. (거짓)
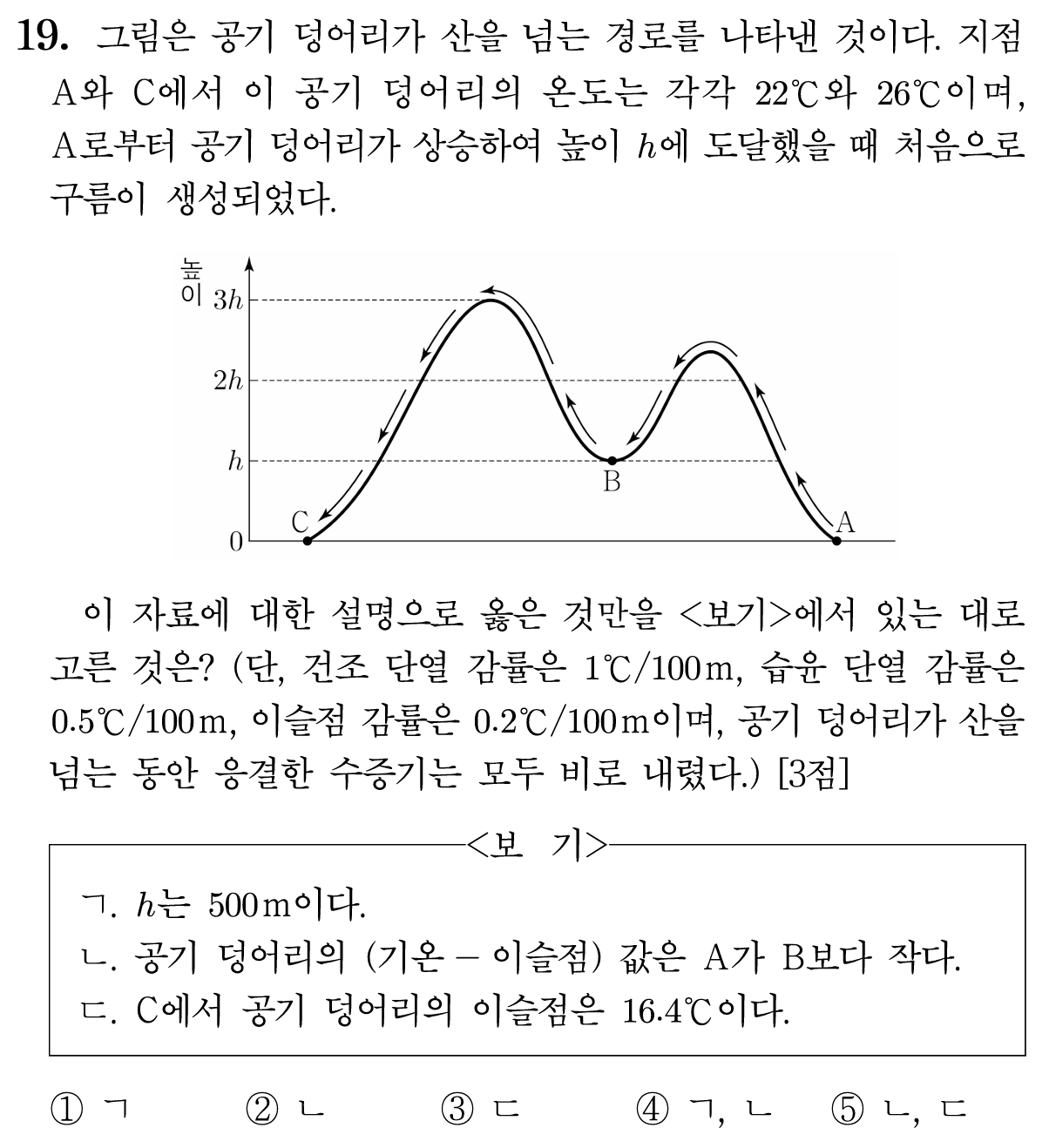
19번 (47%)
푄을 유심히 봤다면 굉장히 빨리 풀 수 있는 문제입니다만, 그렇지 않다면 긴 풀이 시간이 필요했을 것입니다. 해설에서는 일단 그런 긴 풀이를 전부 서술하기는 하겠습니다.
해설
이와 같이 계곡(B)이 있는 문제의 경우, 이 부분을 무시해도 됩니다. 왜냐하면, 계곡으로 하강할 때와 계곡에서 다시 상승할 때 모두 건조 단열 감률로 공기의 온도가 변하기 때문에, 하강과 상승 과정에서의 온도 변화가 서로 상쇄되기 때문입니다. 따라서 그냥 A에서 C로, $3h$만큼의 산을 넘어간다고 봐도 무방한 것이죠.
ㄱ. 위의 논리에 따라 상승 응결 고도가 $h$, 산의 높이가 $3h$인 상황이므로
$$22-10h-5\times(2h)+10\times(3h)=26 ^\circ\mathrm{C} $$
에서 $h=400\;\mathrm{m}$입니다.
ㄴ. 일단 A에서의 상승 응결 고도는 $h$입니다. 그런데 B에서는 어떨까요? 위에서 말했듯 계곡은 무시할 수 있습니다. 계곡으로 하강하는 경우와 계곡에서 상승하는 경우가 상쇄되니까요. 그런 논리로, A와 B 사이의 산 능선에서 B로 내려올 때의 고도 변화량을 $H$라 할 때, B에서 공기 덩어리가 상승하여 응결할 때까지의 고도 변화량은 마찬가지로 $H$입니다.
왜냐하면 공기 덩어리는 $h$에서 응결되어 산 능선까지 (기온 - 이슬점)이 0인 상태로 계속 상승하다가 이후 B까지 $H$만큼 하강하며 기온은 건조 단열 감률로, 이슬점은 이슬점 감률로 증가하며, 다시 $H$만큼 상승하며 기온은 건조 단열 감률로, 이슬점은 이슬점 감률로 감소하기 때문입니다. 즉, 서로 상쇄된다는 뜻입니다.
그래서 결국 B에서 공기덩어리가 상승하여 응결할 때까지의 고도 변화량은 $H$인 반면 A의 상승 응결 고도는 $h$이고, 그림에서 $H>h$입니다. (기온 - 이슬점) 값은 상승응결고도 또는 그 지점에서 공기덩어리가 상승하여 응결할 때까지의 고도 변화량과 정비례하므로, 이 값은 A가 B보다 작습니다.
ㄷ. $3h$ 높이에서 기온과 이슬점이 $26-10\times(3h)=14 ^\circ\mathrm{C} $로 같으므로, C에서의 이슬점은
$$14+2\times(3h)=16.4^\circ\mathrm{C}$$
입니다.

20번 (39%)
ㄴ이 핵심인 문제입니다. 천구를 그리면 굉장히 직관적으로 알 수 있기는 합니다. 20번인만큼 정답률이 꽤 낮게 나왔네요.
해설
적위는 $\mathrm{S}_1$이 $\mathrm{S}_2$보다 작은데도 불구하고 최대 고도가 $80^\circ$로 더 높다는 것은, $\mathrm{S}_1$이 북쪽하늘로 넘어가있다는 의미입니다. 따라서 $\mathrm{S}_1$과 $\mathrm{S}_2$의 적위차가 $10+15=25^\circ$이므로, $\mathrm{S}_2$의 적위는 $+35^\circ$입니다.
ㄱ. $\mathrm{S}_1$과 $\mathrm{S}_2$의 적위차가 $25^\circ$이므로 $\mathrm{S}_2$의 남중고도는 $40+25=65^\circ$입니다. (참)
ㄴ. 천구의 적도와 지평선이 이루는 각이 클수록, 즉 위도가 작을수록 적위가 +인 별이 방위각 $270^\circ$에서 가지는 고도값은 커지게 됩니다. 이는 적위가 +인 별의 동적위선의 위도 변화에 따른 교점이 방위각 $270^\circ$보다 더 큰 방위각에서 발생하고, 이보다 방위각이 작은 부분에서는 위도가 더 작은 지역에서의 동적위선이 위도가 더 큰 지역에서의 동적위선보다 아래에 위치하게 되기 때문입니다.

말을 굉장히 어렵게 쓰긴 했는데, 위와 같이 천구를 그리면 고도 차이를 쉽게 알 수 있습니다. 아무튼 위와 같은 논리에 따라 방위각 $270^\circ$에서 $\mathrm{S}_1$의 고도는 A가 B보다 높습니다. (거짓)
ㄷ. B에서 $\mathrm{S}_2$는 주극성이고, 방위각 $0^\circ$에서 최저고도 $5^\circ$을 갖습니다. 따라서 춘분점이 방위각 $90^\circ$에 있을 때, 방위각 $0^\circ$에 있는 B의 적위는 $6^\mathrm{h}$입니다. (참)
'기타 > 지구과학' 카테고리의 다른 글
| 2024학년도 수능 지구과학2 주요문항 해설 (0) | 2023.11.19 |
|---|---|
| 2023학년도 수능 지구과학2 주요문항 해설 (0) | 2022.11.19 |
| [지2] 천체가 지평선 위에 떠 있는 시간 (0) | 2022.09.17 |
 planetarium
planetarium